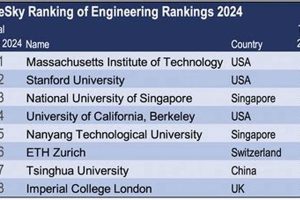
Top-tier institutions for mathematics education offer rigorous curricula, renowned faculty, and cutting-edge research opportunities. These programs often attract highly motivated students and foster a collaborative environment conducive to advanced study in pure mathematics, applied mathematics, and related fields like statistics and computer science. Examples include institutions with dedicated mathematical institutes, strong doctoral programs, and a history of producing influential mathematicians.
A strong mathematics education provides a foundation for critical thinking, problem-solving, and analytical reasoning skills highly valued across diverse industries. Graduates from leading mathematics programs are well-prepared for careers in academia, research, finance, technology, and data science. Historically, centers of mathematical excellence have played a vital role in scientific advancements and technological innovation, shaping our understanding of the world and driving progress.
This article will explore various aspects of identifying and evaluating institutions renowned for their mathematical programs. Factors such as faculty expertise, research output, curriculum design, and career outcomes will be considered to provide a comprehensive overview of what distinguishes exceptional mathematics departments.
Tips for Selecting a Top Mathematics Program
Choosing an institution for advanced mathematical study requires careful consideration of several factors. The following tips offer guidance for prospective students seeking a challenging and rewarding educational experience.
Tip 1: Examine Faculty Research and Expertise: Investigate the research interests of faculty members and assess their contributions to the field. Look for institutions with faculty actively engaged in cutting-edge research and publishing in reputable journals.
Tip 2: Evaluate Curriculum Breadth and Depth: Consider the range of courses offered and the depth of coverage within specific areas of mathematics. A robust program should provide opportunities for specialization and advanced study.
Tip 3: Assess Resources and Facilities: Investigate the availability of computing resources, libraries, and specialized mathematical software crucial for advanced study and research.
Tip 4: Consider Program Size and Student-Faculty Ratio: A smaller program with a low student-faculty ratio can offer more personalized attention and mentorship opportunities.
Tip 5: Explore Career Support and Alumni Network: Investigate career services dedicated to mathematics students and the strength of the alumni network in relevant fields.
Tip 6: Research Funding Opportunities: Explore available scholarships, fellowships, and research assistantships that can provide financial support during studies.
Tip 7: Visit Campuses and Attend Seminars: If possible, visit the campuses of prospective institutions and attend mathematics seminars to gain firsthand experience of the academic environment.
By carefully considering these factors, prospective students can identify programs that align with their academic goals and aspirations, maximizing their potential for success in the field of mathematics.
This exploration of key considerations for selecting a mathematics program provides a framework for informed decision-making. The following conclusion synthesizes these points and offers final recommendations for prospective students.
1. Faculty Expertise
Faculty expertise stands as a cornerstone of any top-tier mathematics program. Distinguished professors, often leaders in their respective research areas, contribute significantly to the quality of education and research opportunities available to students. Their influence shapes curriculum development, ensuring exposure to cutting-edge concepts and methodologies. Moreover, renowned faculty attract substantial research funding, creating opportunities for students to engage in groundbreaking work. For instance, a university with a Fields Medalist on its faculty can offer unparalleled insights into advanced mathematical concepts and foster a stimulating intellectual environment. This, in turn, attracts promising young mathematicians, creating a vibrant academic community.
The presence of expert faculty fosters a culture of rigorous inquiry and intellectual exchange. Students benefit from direct mentorship by leading researchers, gaining invaluable experience in formulating research questions, designing studies, and contributing to new knowledge creation. This close interaction with faculty also opens doors to collaborations with other institutions and researchers, expanding students’ professional networks. Furthermore, faculty expertise influences the development of specialized research centers and initiatives within a mathematics department. For example, a university with faculty specializing in computational mathematics might establish a center dedicated to high-performance computing, providing students with access to advanced resources and expertise.
In conclusion, faculty expertise serves as a critical indicator of a strong mathematics program. Institutions with accomplished faculty offer not only high-quality instruction but also invaluable research opportunities, contributing significantly to student success and advancement in the field. The concentration of expertise within a department often drives innovation and establishes the institution as a leader in specific areas of mathematical research. Therefore, prospective students seeking challenging and rewarding educational experiences should prioritize institutions renowned for their facultys accomplishments and contributions to the field.
2. Curriculum Rigor
Curriculum rigor serves as a defining characteristic of leading mathematics programs. A demanding curriculum exposes students to foundational and advanced concepts, fostering deep understanding and critical thinking skills essential for success in the field. Rigorous programs often incorporate proof-based courses early in the curriculum, emphasizing logical reasoning and abstract thinking. For example, institutions renowned for their theoretical mathematics programs might require abstract algebra and real analysis in the first two years of undergraduate study. This early exposure to abstract concepts cultivates a strong foundation for tackling complex mathematical problems and pursuing advanced research. Such rigor differentiates leading programs from those offering a more general mathematics education.
The intensity of a curriculum also manifests in the depth and breadth of topics covered. Leading programs often offer specialized courses in areas like number theory, topology, and differential geometry, allowing students to delve deeper into specific subfields. Furthermore, a rigorous curriculum frequently incorporates computational components, equipping students with the skills to utilize software and programming languages for mathematical modeling and data analysis. For instance, a program emphasizing applied mathematics might require proficiency in programming languages like Python or R, along with coursework in numerical analysis and scientific computing. This integration of computational skills prepares graduates for careers in data science, finance, and other computationally intensive fields.
In conclusion, curriculum rigor plays a crucial role in shaping successful mathematicians. The challenging nature of these programs cultivates essential skills in abstract reasoning, problem-solving, and computational analysis. By demanding deep engagement with mathematical concepts and methods, these programs prepare graduates for the intellectual demands of advanced study and professional careers. A thorough understanding of curriculum rigor provides valuable insights for prospective students seeking to identify and evaluate top mathematics programs. This focus on rigor often correlates with strong research output and successful alumni outcomes, solidifying the institution’s reputation as a center of mathematical excellence.
3. Research Opportunities
A hallmark of leading mathematics programs lies in the breadth and depth of research opportunities afforded to students. These opportunities provide invaluable experience in applying theoretical knowledge to real-world problems, fostering critical thinking, and contributing to the advancement of the field. Institutions recognized for their strength in mathematics often cultivate a vibrant research environment, characterized by active faculty involvement in cutting-edge projects, well-funded research centers, and ample resources for student participation. For example, a university with a dedicated institute for mathematical modeling might offer undergraduate students the chance to contribute to projects addressing climate change, disease spread, or financial market dynamics. Such experiences not only enhance students’ understanding of mathematical concepts but also provide crucial professional development and networking opportunities.
The quality of research opportunities often correlates with the caliber of faculty expertise. Institutions with renowned mathematicians on their faculty attract substantial research grants and contracts, creating a fertile ground for student involvement. For instance, a university with a faculty member specializing in cryptography might secure funding for research on cybersecurity, providing students with opportunities to contribute to this critical field. Furthermore, institutions with strong research programs often foster collaborations with industry partners, government agencies, and other academic institutions, expanding the scope and impact of research endeavors. This interconnectedness exposes students to diverse perspectives and potential career paths. Students working alongside faculty on externally funded projects gain experience in proposal writing, data analysis, and scientific communication, enhancing their professional portfolios.
In summary, research opportunities serve as a critical component distinguishing exceptional mathematics programs. Access to cutting-edge research projects, mentorship by leading experts, and collaborations with external partners contribute significantly to student development and career preparation. The strength of a program’s research environment often reflects its commitment to advancing mathematical knowledge and fostering the next generation of mathematicians. Therefore, prospective students seeking intellectually stimulating and professionally rewarding experiences should prioritize institutions with thriving research cultures and demonstrable success in securing funding and producing impactful research outcomes.
4. Industry Connections
Strong industry connections represent a critical component distinguishing top mathematics programs. These connections provide students with invaluable practical experience, enhance career prospects, and foster collaborative research opportunities that benefit both academia and industry. Leading mathematics departments actively cultivate relationships with companies in sectors such as finance, technology, data science, and consulting, recognizing the increasing demand for highly skilled mathematicians. For example, partnerships with financial institutions can lead to internships where students apply mathematical modeling techniques to risk assessment and portfolio optimization. Similarly, collaborations with technology companies can involve students in developing algorithms for machine learning or artificial intelligence. Such experiences bridge the gap between theoretical knowledge and practical application, providing students with a competitive edge in the job market.
These partnerships often extend beyond internships to encompass collaborative research projects. Faculty members in top mathematics programs frequently engage in research funded by industry partners, addressing real-world challenges and contributing to innovation. This applied research not only advances mathematical knowledge but also provides students with opportunities to work on projects with direct practical relevance. For instance, a university partnering with a pharmaceutical company might conduct research on optimizing drug delivery systems using mathematical modeling. Students participating in such projects gain valuable experience in applying their skills to complex problems, while also contributing to advancements with tangible societal impact. Furthermore, industry connections can lead to the development of specialized curricula and research centers tailored to industry needs, ensuring that graduates possess the skills and knowledge sought by employers. For example, a university might establish a data science center in partnership with technology companies, offering specialized courses and research opportunities in this rapidly growing field.
In conclusion, robust industry connections significantly enhance the value and reputation of mathematics programs. By providing students with practical experience, fostering collaborative research, and shaping curricula to meet industry demands, these connections contribute to both student success and the advancement of the field. Institutions that prioritize cultivating strong industry ties position their graduates for rewarding careers and establish themselves as key players in driving innovation across diverse sectors. Therefore, the presence of established and active industry partnerships serves as a crucial indicator of a mathematics program’s commitment to providing a comprehensive and relevant education, bridging the gap between academic theory and real-world practice.
5. Alumni Network
A robust and engaged alumni network constitutes a significant asset for institutions recognized for mathematics excellence. This network provides a crucial link between current students and the professional world, offering mentorship, career guidance, and access to a diverse range of opportunities. The strength and breadth of an alumni network significantly influence the trajectory of graduates’ careers and contribute to the overall prestige and impact of the institution.
- Mentorship and Career Guidance
Alumni networks facilitate mentorship programs, connecting current students with experienced professionals in various fields. These mentors offer insights into career paths, provide advice on navigating the job market, and share valuable industry knowledge. For instance, an alumnus working in quantitative finance might mentor a student interested in a similar career, offering guidance on relevant coursework and internship opportunities. This personalized support can prove invaluable in helping students make informed career decisions.
- Networking and Job Opportunities
Alumni networks serve as a powerful networking platform, connecting current students and recent graduates with established professionals in diverse industries. This network can lead to internship and job opportunities, as alumni often play a role in recruitment within their organizations. For example, an alumnus working at a technology company might inform the mathematics department about open positions or refer promising candidates. This direct access to the professional world provides a significant advantage for graduates seeking employment.
- Industry Insights and Trends
Alumni working in various sectors offer current students valuable insights into industry trends, emerging technologies, and the evolving demands of the job market. These insights can inform curriculum development and ensure that students are equipped with the skills and knowledge required for success in their chosen fields. For instance, alumni feedback on the importance of data analysis skills might prompt a mathematics department to incorporate more data science courses into the curriculum. This continuous feedback loop ensures that the program remains relevant and responsive to industry needs.
- Philanthropic Support and Resources
Successful alumni often contribute philanthropically to their alma mater, providing essential funding for scholarships, research initiatives, and infrastructure development. This financial support enhances the resources available to current students and faculty, strengthening the overall quality of the mathematics program. For example, an alumnus might endow a scholarship fund specifically for mathematics students, expanding access to educational opportunities. This philanthropic engagement further strengthens the bond between the institution and its alumni network.
In conclusion, a strong and engaged alumni network represents a crucial element distinguishing top mathematics programs. By providing mentorship, career guidance, networking opportunities, and financial support, the alumni network significantly enhances the educational experience and career prospects of graduates. The success and influence of alumni reflect positively on the institution, reinforcing its reputation for excellence and attracting prospective students seeking a program with a proven track record of producing successful mathematicians.
6. Resources and Facilities
Access to cutting-edge resources and facilities constitutes a critical factor distinguishing top mathematics programs. These resources play a crucial role in supporting both teaching and research, fostering a stimulating intellectual environment, and preparing students for the demands of advanced study and professional careers. Institutions committed to mathematics excellence invest significantly in providing state-of-the-art infrastructure, specialized software, and extensive library collections.
- Advanced Computing Resources
High-performance computing clusters, specialized mathematical software, and data visualization tools are essential for tackling complex mathematical problems and conducting advanced research. Institutions with strong mathematics programs often provide access to dedicated computing resources optimized for mathematical computations. For example, access to supercomputers allows researchers to perform simulations and analyze large datasets, pushing the boundaries of mathematical modeling and data analysis. These resources also support student learning by enabling them to explore complex mathematical concepts through computational experiments and simulations.
- Specialized Libraries and Research Databases
Comprehensive libraries with extensive collections of mathematical journals, books, and research databases are indispensable for both students and faculty. Access to these resources enables in-depth literature reviews, exploration of historical mathematical developments, and investigation of current research trends. For example, a specialized mathematics library might subscribe to rare historical journals or provide access to digital archives of prominent mathematicians’ works. These resources support rigorous scholarship and provide historical context crucial for advanced study.
- Collaborative Workspaces and Research Centers
Dedicated spaces designed to foster collaboration and interaction among students and faculty play a vital role in creating a vibrant intellectual community. These spaces might include seminar rooms, collaborative work areas, and dedicated research centers equipped with specialized tools and resources. For instance, a dedicated research center for topology might house advanced geometric modeling software and provide a space for researchers to collaborate on complex topological problems. These environments facilitate the exchange of ideas, stimulate interdisciplinary research, and foster a sense of belonging among students and faculty.
- State-of-the-art Laboratories and Equipment
While often associated with experimental sciences, specialized laboratories and equipment also play a role in certain areas of mathematical research. For example, institutions with programs in experimental mathematics might have laboratories equipped with tools for visualizing geometric structures or conducting experiments related to number theory. Similarly, departments with a focus on financial mathematics might have dedicated trading rooms equipped with real-time market data feeds and financial modeling software. These specialized resources support research at the intersection of mathematics and other disciplines, broadening the scope of inquiry and providing students with unique research experiences.
In summary, the quality and availability of resources and facilities significantly impact the overall strength and reputation of a mathematics program. Institutions investing in these resources demonstrate a commitment to providing students and faculty with the tools they need to excel in research and education. The presence of state-of-the-art computing infrastructure, comprehensive libraries, collaborative workspaces, and specialized laboratories contributes significantly to the intellectual vitality of a mathematics department and serves as a key factor attracting top talent and driving innovation in the field. Therefore, when evaluating mathematics programs, prospective students and researchers should carefully consider the resources and facilities available, recognizing their crucial role in supporting academic success and fostering a thriving research environment.
Frequently Asked Questions about Top Mathematics Programs
This section addresses common inquiries regarding the pursuit of mathematics education at leading institutions. The responses aim to provide clarity and guidance for prospective students considering advanced study in mathematics.
Question 1: What distinguishes top mathematics programs from others?
Leading programs are characterized by distinguished faculty actively engaged in cutting-edge research, rigorous curricula emphasizing theoretical depth and problem-solving skills, access to advanced resources and facilities, and strong connections to industry and research institutions. These factors combine to create a rich learning environment that fosters intellectual growth and prepares graduates for successful careers.
Question 2: How important is research experience for undergraduate mathematics students?
Research experience is highly valuable for undergraduates. It provides practical application of theoretical knowledge, develops critical thinking skills, and enhances career prospects. Participating in research projects allows students to contribute to new discoveries and gain firsthand experience in the process of mathematical inquiry.
Question 3: What career paths are common for graduates of top mathematics programs?
Graduates pursue diverse career paths, including academia, research, finance, technology, data science, and consulting. The strong analytical and problem-solving skills cultivated in these programs are highly sought after across various industries.
Question 4: How does one identify faculty expertise within a mathematics department?
Examining faculty profiles on departmental websites, reviewing publications in reputable journals, and investigating research grants and awards can provide insights into faculty expertise. Attending departmental seminars and conferences can offer further opportunities to assess faculty research interests and contributions to the field.
Question 5: What role does curriculum rigor play in shaping successful mathematicians?
A rigorous curriculum fosters deep understanding of fundamental mathematical concepts and develops critical thinking skills essential for advanced study and research. Exposure to challenging problems and proof-based courses cultivates the ability to think abstractly and rigorously, preparing students for the intellectual demands of the field.
Question 6: How do industry connections benefit students in mathematics programs?
Industry connections provide students with practical experience through internships, collaborative research projects, and networking opportunities. These connections bridge the gap between theoretical knowledge and real-world application, enhancing career prospects and providing valuable insights into industry trends.
These responses provide a starting point for understanding the key elements of successful mathematics programs. Thorough research and careful consideration of individual academic goals are crucial for making informed decisions about pursuing advanced mathematical study.
The following section will delve further into specific examples of institutions renowned for their mathematics programs, providing concrete examples of the principles discussed here.
Conclusion
Institutions renowned for mathematics excellence offer a unique combination of factors that contribute to a superior educational experience. Distinguished faculty, rigorous curricula, robust research opportunities, strong industry connections, vibrant alumni networks, and state-of-the-art resources collectively cultivate an environment conducive to profound intellectual development and successful career trajectories. Understanding these interconnected elements provides a framework for evaluating and selecting programs best suited to individual academic and professional goals. The pursuit of a mathematics education at a leading institution represents a substantial investment in intellectual growth, promising both challenging academic experiences and rewarding career prospects.
The landscape of mathematics continues to evolve, driven by ongoing research and its expanding applications across diverse fields. Selecting an institution committed to fostering future generations of mathematicians requires careful consideration of its commitment to innovation, collaboration, and rigorous scholarship. By seeking programs that embody these values, aspiring mathematicians position themselves to contribute meaningfully to the advancement of the field and its continued impact on society.